iTransformer implementation in pure Rust

What is iTransformer?

iTransformer represents a groundbreaking deep learning architecture specifically tailored for multivariate time series forecasting (MTSF). Unlike traditional Transformers that are predominantly applied to sequential data like text or image patches, iTransformer adapts the Transformer paradigm to time series forecasting by treating each variate (feature) as an independent token. This enables it to capture intricate inter-variate relationships alongside temporal dependencies, making it exceptionally powerful for high-dimensional data.

Why Multivariate Time Series Forecasting?

Forecasting time series with multiple features is pivotal in many domains, including:

Finance: Predicting complex market behaviors, such as stock trends or volatility indices.
Energy Systems: Managing energy demand, predicting consumption patterns, or renewable energy generation.
Meteorology: Simultaneously modeling temperature, pressure, and other meteorological factors.
Transportation Systems: Understanding vehicle traffic patterns and forecasting congestion.

In contrast to univariate time series forecasting, which focuses solely on a single feature, multivariate forecasting requires a nuanced understanding of how features interact over time. Capturing both temporal and inter-variate dependencies is critical, and iTransformer excels in this area.

Theoretical Foundations of iTransformer

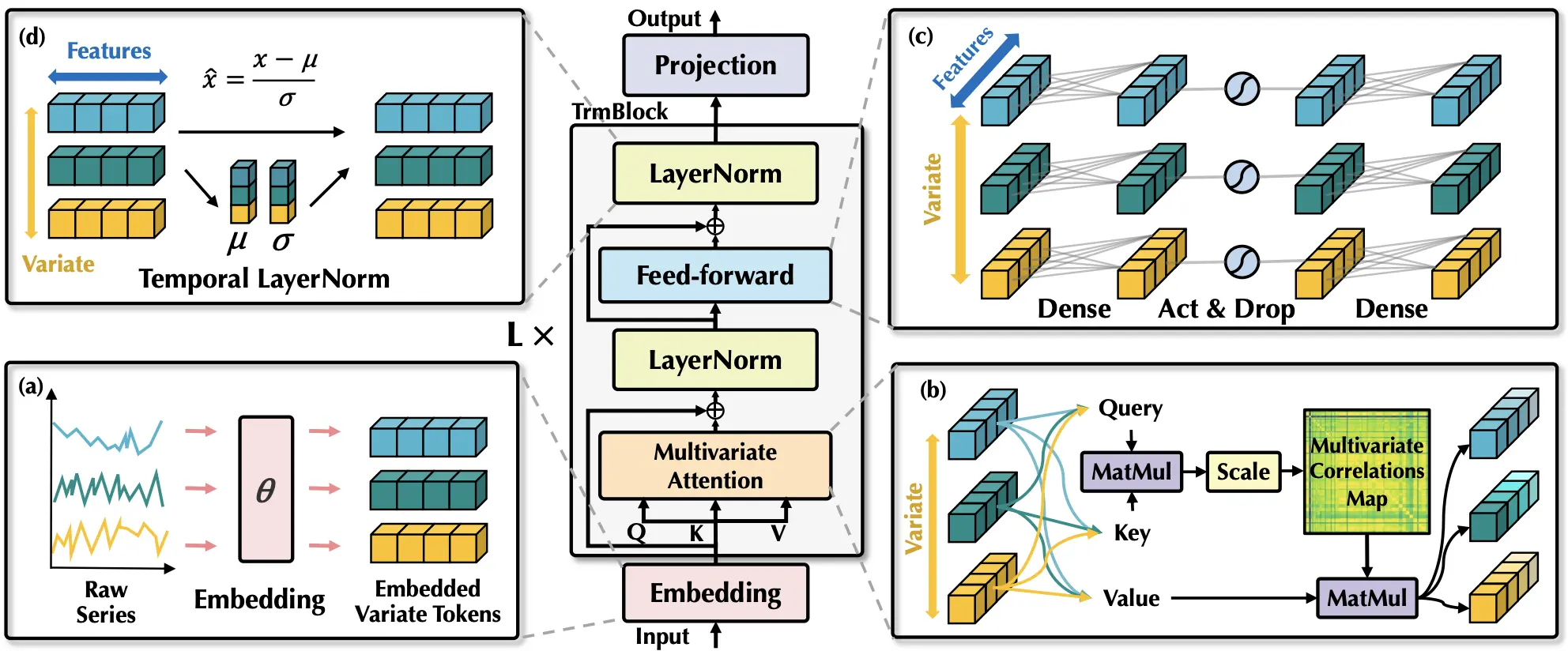
The iTransformer architecture reimagines the Transformer model by reversing its application to time series. Below is an in-depth analysis of its key components and differences compared to traditional Transformers.

Traditional Transformer vs. iTransformer

Data Representation

Traditional Transformers process sequential tokens, such as words in a sentence, with the sequence length forming the primary dimension of attention. For a multivariate time series $X \in\mathbb{R}^{T \times N}$ , where:

$T$ is the temporal dimension (sequence length), and
$N$ is the number of variates (features),

traditional approaches flatten $X$ into a sequence of $T \times N$ tokens or process each feature independently over time, often losing inter-variate relationships.

In iTransformer, the input matrix is transposed to $X^\top \in \mathbb{R}^{N \times T}$ . Each variate becomes a token, and the temporal dimension $T$ is embedded implicitly. This allows iTransformer to model relationships between variates explicitly, a fundamental departure from conventional Transformers.

Embedding Layer

Each variate $x_n$ is mapped into a higher-dimensional representation using a Multi-Layer Perceptron (MLP):

$\left[ H^0 = \text{MLP}(X), \quad H^0 \in \mathbb{R}^{N \times D} \right]$

Here, $D$ represents the token embedding dimension. This embedding encodes both temporal information and feature-specific characteristics, setting the stage for subsequent attention layers.

Attention Mechanism

The self-attention mechanism in iTransformer focuses on capturing inter-dependencies across variates. For a given layer $l$ , self-attention updates the representation of each variate token $H^{l-1}$ :

$\left[ H^{l-1} \leftarrow \text{LayerNorm}\left(H^{l-1} + \text{Self-Attn}(H^{l-1})\right) \right]$

The self-attention operation computes scaled dot-product attention:

$\left[ \text{Attention}(Q, K, V) = \text{softmax}\left(\frac{QK^\top}{\sqrt{d_k}}\right)V \right]$

where $(Q,K,V4)$ represent the query, key, and value matrices derived from $H^{l-1}$ . This mechanism ensures that each variate token integrates information from all other variates, effectively capturing their dependencies.

Feed-Forward Network (FFN)

After self-attention, a position-wise feed-forward network refines the representation of each variate independently:

$\left[ H^l \leftarrow \text{LayerNorm}\left(H^{l-1} + \text{Feed-Forward}(H^{l-1})\right) \right]$

The FFN consists of two linear transformations with a non-linear activation (e.g., GELU) in between, enhancing feature-specific representations.

Hierarchical Representation

By stacking multiple layers of self-attention and feed-forward blocks, iTransformer constructs hierarchical representations that jointly encode temporal patterns and inter-variate relationships. The depth $L$ determines the capacity of the model to capture complex dependencies.

Output Projection

The final output representation $H^L$ is projected back into the time series space through another MLP:

$\left[ \hat{Y} = \text{MLP}(H^L), \quad \hat{Y} \in \mathbb{R}^{S \times N} \right]$

Here, $S$ denotes the prediction horizon, i.e., the number of future timesteps to forecast. The predicted matrix is then transposed back to align with the original input shape.

Algorithmic Description

The following formal algorithm describes the iTransformer workflow:

This algorithm encapsulates the essence of iTransformer, detailing its inversion of the traditional Transformer paradigm to better suit multivariate time series data.

Rust Implementation

The iTransformer architecture has been implemented in Rust, leveraging its high-performance capabilities and memory safety. Below is a detailed explanation of the implementation.

GitHub Repository

Explore the full implementation at iTransformer on GitHub.

Installation

To use iTransformer in your Rust project, include it as a dependency in your Cargo.toml:

[dependencies]
itransformer = "1.0.0"

Key Components

iTransformer's Rust implementation mirrors its theoretical design, with components that map directly to the model's architecture.

Core Struct: `ITransformer`

The main struct defines the architecture, including parameters for the number of variates, lookback length, depth, token dimensions, and attention mechanisms.

#[derive(Debug)]
pub struct ITransformer {
    num_variates: i64,
    lookback_len: i64,
    pred_length: Vec<i64>,
    num_tokens_per_variate: i64,
    mem_tokens: Option<Tensor>,
    reversible_instance_norm: Option<RevIn>,
    layers: Vec<(Attention, FeedForward)>,
    mlp_in: MlpIn,
    pred_heads: Vec<PredHead>,
}

Example Usage

The following example demonstrates how to initialize and use iTransformer in Rust:

use tch::{Device, Tensor, nn::VarStore, Kind};

fn main() -> Result<(), Box<dyn std::error::Error>> {
    let vs = VarStore::new(Device::Cpu);
    let model = ITransformer::new(
        &(vs.root() / "itransformer"),
        137, // Number of variates
        96,  // Lookback length
        6,   // Depth of Transformer blocks
        256, // Hidden dimension
        Some(1),       // Tokens per variate
        vec![12, 24, 36, 48], // Prediction lengths
        Some(64),     // Dimension of each attention head
        Some(8),      // Number of attention heads
        None,         // Attention dropout probability
        None,         // Feed-forward multiplier
        None,         // Feed-forward dropout probability
        None,         // Number of memory tokens
        Some(true),   // Use reversible instance normalization
        None,         // Reversible normalization affine
        false,        // Use FlashAttention
        &Device::Cpu,
    )?;

    let time_series = Tensor::randn([2, 96, 137], (Kind::Float, Device::Cpu));
    let preds = model.forward(&time_series, None, false);
    println!("{:?}", preds);
    Ok(())
}

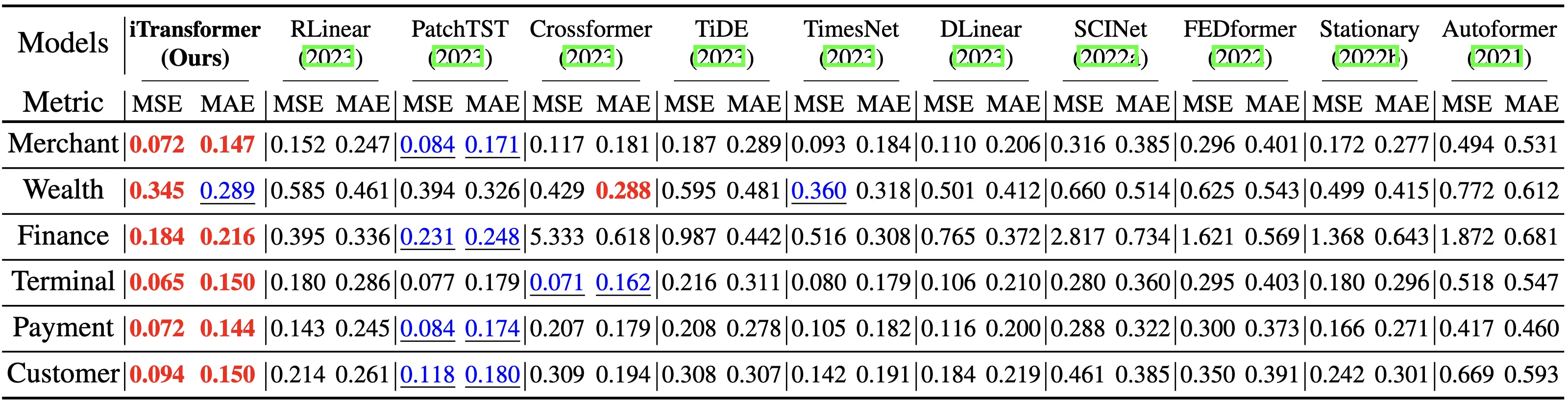
Main Result of Multivariate Forecasting

The iTransformer was evaluated on challenging multivariate forecasting benchmarks (generally hundreds of variates). The main result can be found in the table and further benchmarks under the GitHub repository of the original implementation. Comprehensive good performance (MSE/MAE $\downarrow$ ) is achieved.