Deep Learning the Volatility Surface: An AI-Enhanced Calibration of the Heston Model
by Daniel Boros
Nov 9
10 min read
563 views
In quantitative finance, accurately modeling the volatility surface is crucial for option pricing, risk management, and derivative structuring. The Heston model, a popular stochastic volatility model, extends the Black-Scholes-Merton framework by incorporating a stochastic process for volatility. However, calibrating the Heston model to market data can be computationally intensive due to the complexity of the pricing function and the need for repeated evaluations during optimization. Recent advancements suggest that deep learning can significantly enhance this process. By approximating the implied volatility surface using neural networks, we can achieve faster calibration without sacrificing accuracy.
This post delves into an AI-based approach for fitting the volatility surface under the Heston model, inspired by the research paper Deep Learning Volatility by Horvath, Muguruza, and Tomas. We will explore how a neural network can be trained to approximate the implied volatility function, thereby bypassing the need for expensive numerical simulations during calibration. We compare this method with traditional analytical calibration, include mathematical formulations, and provide Rust code implementations. All the code is open source and available in the stochastic-rs library.
Visualization of the Fitting Results
To demonstrate the effectiveness of our neural network model in approximating the implied volatility surface, we present a visualization comparing the actual implied volatilities with those predicted by the neural network after training. The graph illustrates the results of the fitting process, showcasing how well the model has learned the complex relationship between the Heston model parameters and the implied volatilities across different strikes and maturities.
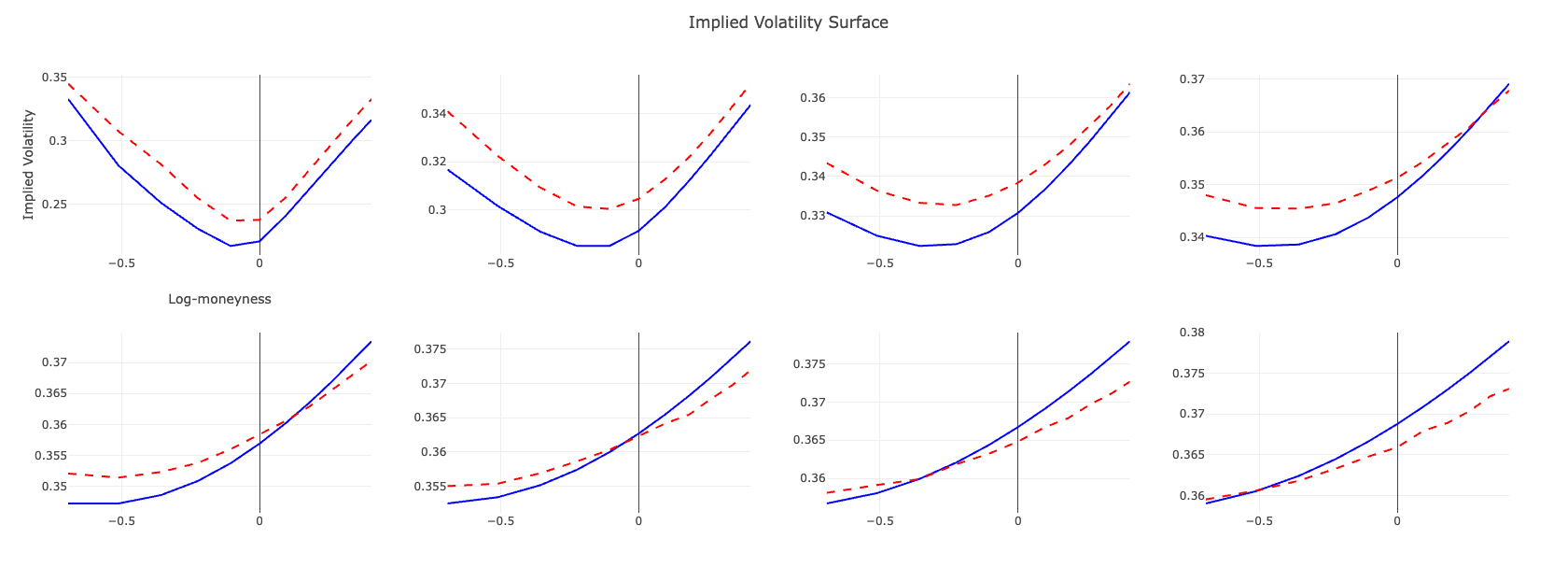
Figure: The plot displays the actual implied volatilities (solid lines) and the predicted implied volatilities from the neural network (dashed lines) for various maturities and strikes. The close alignment between the two sets of curves indicates that the neural network has successfully captured the dynamics of the volatility surface, achieving a high level of accuracy in the fitting process.
By closely matching the predicted volatilities to the actual market data, the neural network demonstrates its capability to serve as an efficient and accurate surrogate for the computationally intensive pricing function in the Heston model. This visual confirmation underscores the potential of deep learning techniques in enhancing financial models and streamlining calibration procedures.
Summary of Training Progress
The table below summarizes the MSE values at each epoch during the training process:
| Epoch | Train MSE | Test MSE |
|---|---|---|
| 1 | 0.15654 | 0.16118 |
| 2 | 0.09154 | 0.09467 |
| 3 | 0.06490 | 0.06684 |
| ... | ... | ... |
| 100 | 0.00209 | 0.00246 |
| ... | ... | ... |
| 200 | 0.00150 | 0.00185 |
Table 1: MSE values for training and test datasets over 200 epochs.
As observed, both the training and test MSE decrease significantly over the epochs, indicating that the model is effectively learning to approximate the implied volatility surface.
Let's Dive into the Technical Details
The Heston model is widely used for pricing European options, as it captures the stochastic nature of volatility observed in real markets. The model is defined by a set of stochastic differential equations (SDEs) that describe the dynamics of the asset price and its variance:
where:
- is the asset price at time .
- is the stochastic variance.
- is the drift term (often set to the risk-free rate in risk-neutral valuation).
- is the mean reversion rate of the variance.
- is the long-term variance (mean reversion level).
- is the volatility of volatility.
- and are Wiener processes with correlation .
This model accounts for the mean-reverting nature of volatility and allows for a correlation between the asset price and its volatility, which is observed in empirical data.
Calibrating the Heston model involves finding the parameter vector such that the model prices match the observed market prices . This requires solving an optimization problem:
where is a suitable distance metric, such as the least squares error. Traditional calibration methods, like the Levenberg-Marquardt algorithm, necessitate numerous evaluations of the pricing function at different parameter values. Each evaluation can be computationally expensive because the Heston pricing function involves complex integrals and characteristic functions, making the entire calibration process time-consuming and sensitive to initial parameter estimates.
To overcome these challenges, we adopt a neural network approach inspired by Horvath et al.'s work. The key idea is to separate the approximation of the implied volatility function from the calibration procedure. By training a neural network to map model parameters directly to the implied volatility surface, we can replace the computationally intensive pricing function with a fast and accurate approximation. The calibration then becomes a deterministic optimization problem using this neural network, significantly speeding up the process.
Mathematically, we define our model with parameters , and a pricing map , where represents the set of financial contracts (e.g., options with different strikes and maturities). We aim to train a neural network such that:
and the approximation error satisfies:
where is an acceptable error margin. The neural network must achieve approximation errors comparable to the original numerical methods, like Monte Carlo simulations, while providing significant speedups in functional evaluations.
Implementing this approach requires generating a synthetic dataset of Heston model parameters and their corresponding implied volatilities. We simulate a wide range of parameter combinations within realistic bounds and compute the implied volatilities for a grid of strikes and maturities using numerical methods. This dataset serves as the training data for the neural network.
We use Rust and the candle crate for deep learning to implement the neural network. The model architecture consists of an input layer that accepts the Heston model parameters, three hidden layers with Exponential Linear Unit (ELU) activation functions, and an output layer that produces the implied volatilities for the specified grid.
Here is the Rust code for the neural network model:
use candle_core::{DType, Device, Result, Tensor};
use candle_nn::{linear, AdamW, Linear, Module, Optimizer, ParamsAdamW, VarBuilder, VarMap};
/// Neural Network Model for Implied Volatility Surface Approximation
pub struct Model {
linear1: Linear,
linear2: Linear,
linear3: Linear,
output_layer: Linear,
}
impl Model {
pub fn new(
vs: VarBuilder,
input_dim: usize,
hidden_size: usize,
output_dim: usize,
) -> Result<Self> {
let linear1 = linear(input_dim, hidden_size, vs.pp("linear-1"))?;
let linear2 = linear(hidden_size, hidden_size, vs.pp("linear-2"))?;
let linear3 = linear(hidden_size, hidden_size, vs.pp("linear-3"))?;
let output_layer = linear(hidden_size, output_dim, vs.pp("linear-4"))?;
Ok(Self {
linear1,
linear2,
linear3,
output_layer,
})
}
}
impl Module for Model {
fn forward(&self, xs: &Tensor) -> Result<Tensor> {
let xs = self.linear1.forward(&xs)?.elu(2.0)?;
let xs = self.linear2.forward(&xs)?.elu(2.0)?;
let xs = self.linear3.forward(&xs)?.elu(2.0)?;
let xs = self.output_layer.forward(&xs)?;
Ok(xs)
}
}
Before training the model, we scale the parameters and implied volatilities to improve the efficiency and convergence of the training process. We use custom scaling functions for the parameters and a standard scaler for the implied volatilities. The scaling ensures that all input features are on a similar scale, which is essential for neural network training.
fn scale_parameters(array: &Array2<f64>, lb: &[f64; 5], ub: &[f64; 5]) -> Array2<f64> {
let scaled_rows: Vec<Array1<f64>> = array
.axis_iter(Axis(0))
.map(|row| myscale(&row.to_owned(), lb, ub))
.collect();
stack(
Axis(0),
&scaled_rows.iter().map(|row| row.view()).collect::<Vec<_>>(),
)
.expect("Failed to stack arrays")
}
struct StandardScaler2D {
mean: Array1<f64>,
std: Array1<f64>,
}
impl StandardScaler2D {
fn fit(data: &Array2<f64>) -> Self {
let mean = data.mean_axis(Axis(0)).unwrap();
let mut std = data.std_axis(Axis(0), 0.0);
std = std.mapv(|x| if x == 0.0 { 1e-8 } else { x });
Self { mean, std }
}
fn transform(&self, data: &Array2<f64>) -> Array2<f64> {
(data - &self.mean) / &self.std
}
fn inverse_transform(&self, data: &Array2<f64>) -> Array2<f64> {
data * &self.std + &self.mean
}
}
The training process involves minimizing the mean squared error between the predicted and actual implied volatilities. We use the Adam optimizer with appropriate parameters to update the network weights. The training loop iterates over batches of data for a specified number of epochs, printing out the training and test losses at each epoch.
pub fn train(
dataset: DataSet,
device: &Device,
input_dim: usize,
hidden_size: usize,
output_dim: usize,
batch_size: usize,
epochs: usize,
) -> Result<Model> {
let x_train = dataset.x_train.to_device(device)?;
let y_train = dataset.y_train.to_device(device)?;
let varmap = VarMap::new();
let vs = VarBuilder::from_varmap(&varmap, DType::F32, device);
let model = Model::new(vs, input_dim, hidden_size, output_dim)?;
let optimizer_params = ParamsAdamW {
lr: 1e-3,
beta1: 0.9,
beta2: 0.999,
eps: 1e-7,
weight_decay: 0.0,
};
let mut adam = AdamW::new(varmap.all_vars(), optimizer_params)?;
let x_test = dataset.x_test.to_device(device)?;
let y_test = dataset.y_test.to_device(device)?;
let num_batches = (x_train.dim(0)? + batch_size - 1) / batch_size;
for epoch in 1..=epochs {
for batch_idx in 0..num_batches {
let start = batch_idx * batch_size;
let end = ((start + batch_size).min(x_train.dim(0)?)) as usize;
let current_batch_size = end - start;
let x_batch = x_train.narrow(0, start, current_batch_size)?;
let y_batch = y_train.narrow(0, start, current_batch_size)?;
let logits = model.forward(&x_batch)?;
let loss = candle_nn::loss::mse(&logits, &y_batch)?;
adam.backward_step(&loss)?;
}
// Compute and print the loss on the entire training and test set
let logits = model.forward(&x_train)?;
let loss = candle_nn::loss::mse(&logits, &y_train)?;
let test_logits = model.forward(&x_test)?;
let test_loss = candle_nn::loss::mse(&test_logits, &y_test)?;
println!(
"Epoch: {epoch:3} Train MSE: {:8.5} Test MSE: {:8.5}",
loss.to_scalar::<f32>()?,
test_loss.to_scalar::<f32>()?
);
}
Ok(model)
}
After training the model, we evaluate its performance by comparing the predicted implied volatilities with the actual values on a test dataset. We select a sample from the test set and use the trained neural network to predict the implied volatilities. We then inverse-transform the scaled values to obtain the actual implied volatilities.
// Sample index for plotting
let sample_idx: usize = 1250;
// Get the sample parameters and inverse-transform
let y_sample = y_test_scaled.slice(s![sample_idx, ..]).to_owned();
let y_sample_tensor = Tensor::from_slice(
y_sample.mapv(|v| v as f32).as_slice().unwrap(),
(1, y_sample.len()),
&Device::Cpu,
)?;
// Predict implied volatilities
let y_pred_tensor = model.forward(&y_sample_tensor)?;
let y_pred_vec = y_pred_tensor.get(0)?.to_vec1::<f32>()?;
let prediction = Array1::from(y_pred_vec).mapv(|v| v as f64);
let prediction = scaler.inverse_transform1d(&prediction);
// Get the actual implied volatilities for comparison
let x_sample = x_test.slice(s![sample_idx, ..]).to_owned();
let x_sample = scaler.inverse_transform1d(&x_sample);
To visualize the results, we use the plotly crate to create a plot comparing the actual implied volatilities with those predicted by the neural network across different strikes and maturities. This visualization helps assess the model's performance and highlights any discrepancies between the predicted and actual values.
fn plot_results_with_plotly(
strikes: &Array1<f64>,
maturities: &Array1<f64>,
actual: &Array1<f64>,
prediction: &Array1<f64>,
) -> Result<()> {
let strikes_dim = strikes.len();
let s0 = 1.0;
let mut plot = Plot::new();
for (i, &maturity) in maturities.iter().enumerate() {
let start = i * strikes_dim;
let end = start + strikes_dim;
let log_moneyness = strikes.iter().map(|&k| (k / s0).ln()).collect::<Vec<f64>>();
let actual_slice = actual.slice(s![start..end]).to_vec();
let prediction_slice = prediction.slice(s![start..end]).to_vec();
let trace_actual = Scatter::new(log_moneyness.clone(), actual_slice)
.name(format!("Actual - Maturity {:.2}", maturity))
.mode(Mode::Lines)
.line(plotly::common::Line::new().color("blue"))
.show_legend(i == 0);
let trace_prediction = Scatter::new(log_moneyness.clone(), prediction_slice)
.name(format!("Prediction - Maturity {:.2}", maturity))
.mode(Mode::Lines)
.line(
plotly::common::Line::new()
.dash(plotly::common::DashType::Dash)
.color("red"),
)
.show_legend(i == 0);
plot.add_trace(trace_actual);
plot.add_trace(trace_prediction);
}
plot.show();
Ok(())
}
The neural network approach offers significant advantages over traditional calibration methods. By replacing the computationally intensive pricing function with a neural network approximation, we eliminate the bottleneck caused by repeated evaluations during optimization. The neural network provides instant functional evaluations, allowing for efficient exploration of the parameter space during calibration.
Moreover, the neural network achieves approximation errors comparable to Monte Carlo methods but at a fraction of the computational cost. As demonstrated in Horvath et al.'s paper, the neural network provides a speedup of approximately 9,000 to 16,000 times compared to Monte Carlo simulations when evaluating the full implied volatility surface. This substantial speedup enables real-time calibration, which is particularly valuable in fast-paced trading environments.
Separating the implied volatility approximation from the calibration procedure also enhances the flexibility and robustness of the method. Evaluating the implied volatility surface across a grid ensures that different parameter combinations produce distinct outputs, improving injectivity and reducing the risk of multiple parameter sets yielding similar prices.
In conclusion, by leveraging deep learning, we can effectively approximate the implied volatility surface under the Heston model, offering a faster and equally accurate alternative to traditional calibration methods. This approach not only accelerates the calibration process but also maintains the robustness and reliability required in financial modeling.
References
-
Horvath, B., Muguruza, A., & Tomas, M. (2019). Deep Learning Volatility. arXiv preprint arXiv:1901.09647. DOI: 10.48550/arXiv.1901.09647
-
Heston, S. L. (1993). A Closed-Form Solution for Options with Stochastic Volatility with Applications to Bond and Currency Options. The Review of Financial Studies, 6(2), 327–343.